When we introduced Correlated Outcomes last week, we mentioned that enabling correlation actually increases uncertainty. This counter-intuitive impact warranted some more examination so you can understand what is happening.
Defining Uncertainty
When it comes to simulations, uncertainty is how tightly packed the outcomes are. For our case, we'll use the middle 80% range.
Simple Simulation
We'll use a simple project simulation, the same as we brought our for our post on the curse of parallel tasks.
Results
For each correlation level, the simulation is run at 100,000 runs in DartCannon to give the following results:
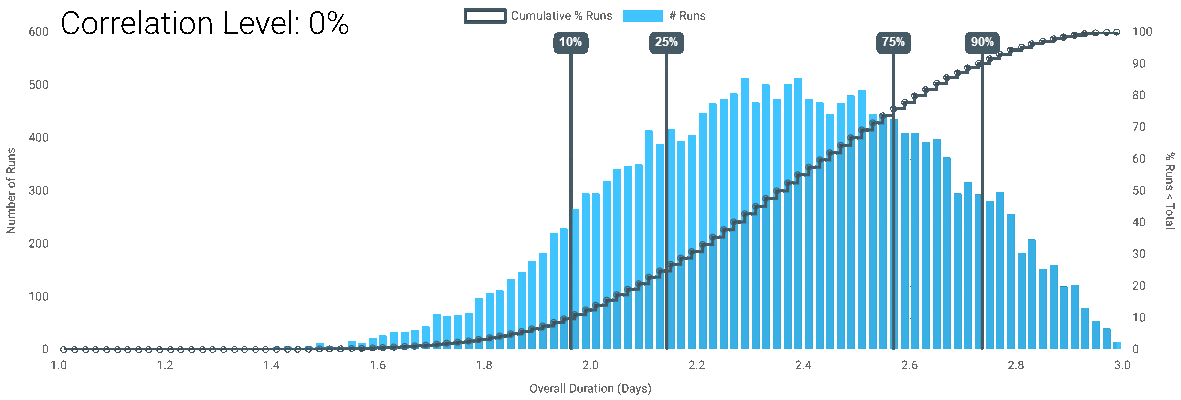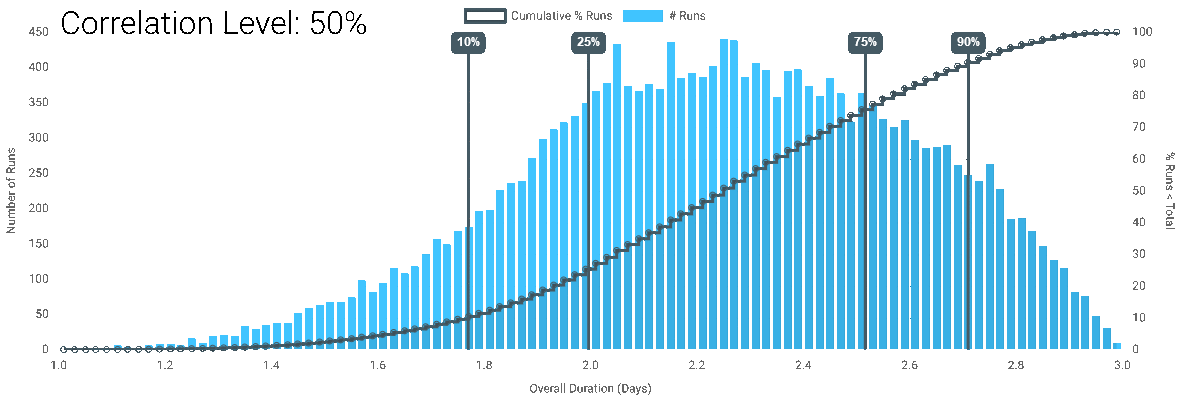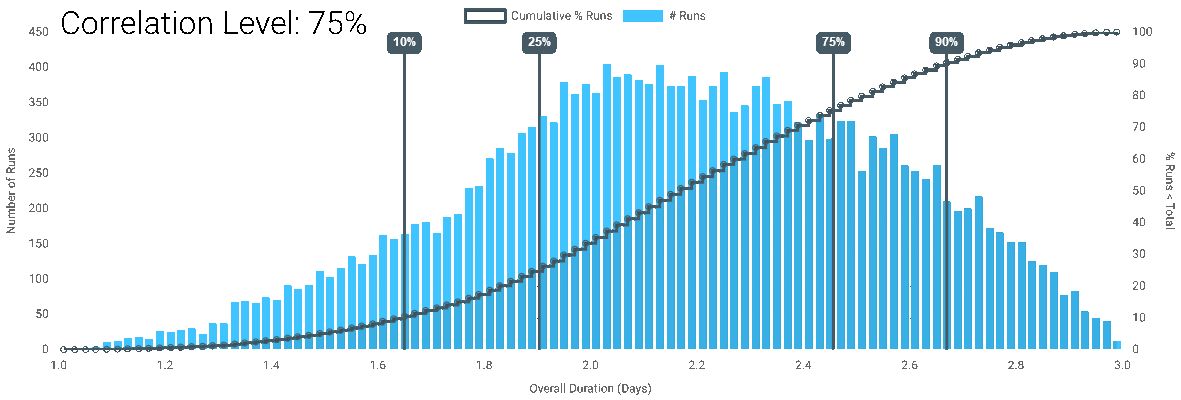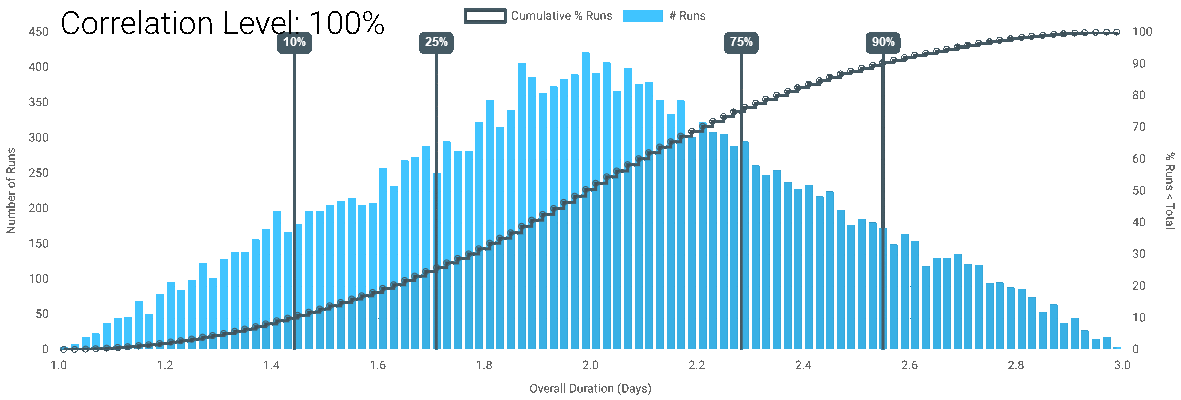
| Correlation Level | Center 80% Range | Center 80% Size | 50% Point |
|---|---|---|---|
| 0% | Between 1.96 Days and 2.74 Days | 0.78 | 2.36 |
| 25% | Between 1.87 Days and 2.73 Days | 0.86 | 2.31 |
| 50% | Between 1.77 Days and 2.71 Days | 0.94 | 2.26 |
| 75% | Between 1.66 Days and 2.68 Days | 1.02 | 2.18 |
| 90% | Between 1.57 Days and 2.64 Days | 1.07 | 2.10 |
| 100% | Between 1.44 Days and 2.55 Days | 1.11 | 2.00 |
Observations
- The Min - Max range is the same for all correlation levels.
- While there is a change for any change in level, the impact is most drastic at the largest levels.
- The higher the correlation, the greater the center 80% range.
- At 100% correlation, the outcome is the same as it would be for a single task.
- For this particular simulation, the center of the results shifts, reversing the effect we described in The Curse of Parallel Tasks.
Discussion
Increasing Uncertainty
To understand the increase in uncertainty, there is a fairly straight-forward way to get an intuitive grasp on the situation. It takes a few steps, but understanding correlations will help understand Monte Carlo simulations in general.
First, the more items in a simulation, either line items or tasks, causes a tighter output compared to the total range. Consider the dice example from My First Monte Carlo - results cluster in the center as there are more ways to create those outcomes, with one high and the other low. The same situation exists in more complex simulations.
Also, correlated outcomes undoes that complexity. In this simple simulation, as we increase correlation, the results get closer and closer to the result from a project with a single task. While a more complex project network wouldn't look like a single task, the idea holds that complexity is reduced.
Taken together, these two ideas show how correlation changes the final uncertainty.
Change in 50% point
This particular outcome does not generalize as obviously as the increase in uncertainty. While in this specific simulation, you can think through how the change to resemble a single task would impact the center, that will break down as simulation complexity increases.
This outcome emphasizes the importance of simulating your outcomes. As we mentioned in the curse of parallel tasks, while possible to intuit individual effects in a simulation, it doesn't take much complexity to make 'thinking it through' practically impossible.
Correlated Outcomes is a Pro feature - Sign up today to get access to correlated outcomes and all the other Pro features.
Photo by Davide Foti on Unsplash